Электронная библиотека
публикации о музее-заповеднике «Кижи»

Аннотация: Рассмотрены возможности применения статистических подходов к созданию методов поиска наиболее полного приближения к аутентичности геометрии элементов деревянных памятников. Данная проблема является актуальной для воссоздания аутентичной микро-тектоники и ритмики как основы архитектурного образа деревянных памятников. Проблема рассматривается, в частности, на примере Кижей.

Ключевые слова: деревянное зодчество; технологии реставрации; методы статистического анализа геометрии деревянных деталей; Кижи; Карелия;

Summary:  Possibilities of application of statistical approaches to creation of methods of search of the fullest approach to authenticity of geometry of elements of wooden monuments are considered. This problem is relevant for the reconstruction of authentic micro-tectonics and rhythmics as the basis of the architectural image of wooden monuments. The problem is considered, in particular, on the example of Kizhi.

Keywords: wooden architecture; restoration technologies; methods of statistical analysis of the geometry of wooden parts; Kizhi; Karelia;

1. Деревянное зодчество в современности: между внешним подражательством и заново рождающимся пониманием

Не повторяя общеизвестных высказываний о работах А.В. Ополовникова, отметим следующее. [1] Словно предчувствуя переход к совершенно иной ментальности общества, он сделал важный выбор между формальной, но вполне по-своему легитимной подлинностью деревянных храмов-памятников по состоянию на кон. XIX – нач. ХХ вв., и старинной архитектурно-художественной образной системой (в сущности средневековой). Старинная (или средневековая) система имеет, как известно, весьма характерный и неповторимый способ организации микро-тектоники и микро-ритмики декоративных элементов, вкупе с организацией ритмики бревенчатых срубов и конструкций.

Нисколько не смешивая воедино реставрацию и строительство новых храмов из дерева, все же необходимо сказать несколько слов. В современности дерево как «физический» материал строительства все менее значимо. Можно найти на замену бревну деревянные (или вовсе иные) композитные материалы, соединять детали современными элементами и пр. Слова «деревянный храм», «памятник деревянного зодчества» и их аналоги все меньше означают вещество храма (памятника) и все полнее становятся синонимами понятия «архитектурно-художественный образ» – как исторический в прямом смысле, т.е. объект реставрации, так и вновь проектируемый образ.

Еще вполне объяснимое в XIX – нач. ХХ века подражательство, т.е. приблизительное и неглубокомысленное повторение «традиционных форм», в современности уже становится серьезнейшей проблемой нового проектирования, по вышеназванным причинам. Но и реставрационные технологии также не защищены полностью от таких «веяний времени», как упрощение или утрата «мелкого штриха» на малоприметных уровнях. Цельность архитектурно-художественного образа может быть значительно искажена суммой неточных (или «неаутентичных» в современной терминологии) штрихов деревянных деталей.

Имеющийся богатейший материал Кижей позволяет изучить названные нюансы форм деревянных деталей благодаря сопоставлению результатов реставрации А.В.Ополовникова и наглядно представленным современным реставрационным наработкам. Далее, используя такие серьезные источники, как Кижи, можно постепенно переходить к анализу других объектов, в том числе и объектов современного зодчества.

2. Поиск методов и критериев для анализа названных проблем

Характеристики деревянных элементов на уровне визуального (словесного) описания могут потенциально быть применимы к данному направлению. Но, оставаясь лишь качественными, они существенно уступают статистическим методам. Применение тех или иных стандартизованных приемов (совершенно очевидно, что прежде всего из области непараметрической статистики) в принципе позволяет подойти к созданию системы компьютерных графо-аналитических инструментов распознавания характеристических черт геометрии деревянных элементов. В данном направлении автором были предприняты небольшие предварительные шаги. [2]

Вопрос применения статистических методов как готового алгоритма, который нуждался бы только лишь в программной обработке для перевода в общепригодный компьютерный инструмент, пока не стоит. Актуальным на сегодняшний день является вопрос пробных анализов общедоступных образцов элементов деревянного зодчества, с целью выработки методологии применения тех ли иных непараметрических методов в указанных целях.

На первый план при разборе данных задач выходят методы простейшей ранговой статистики. Наиболее широко распространенные методы и приемы непараметрического анализа, как критерий Манна-Уитни, хорошо работают с численными величинами. Применительно к задаче анализа форм (в простейшем случае, например, лемеха «городком») невозможно свести все операции только к анализу чисел – либо эти числа должны быть отражением как общей геометрии формы, так и «геометрии штриха», или «почерка», которым выполнена конкретная форма.

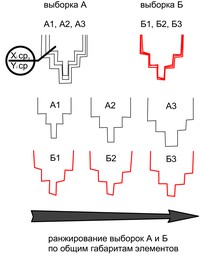
Рис. 1. Пример составления массива данных X’, Y’, выборка А, и X’’, Y’, выборка Б, для лемеха «городком» (абстрактно). Для каждой равнозначной (т.е. соответствующей одному и тому же излому формы) точки можно вычислить среднее X i ср, Y i ср, но без ранжирования с увеличением количества образцов возможность выявить разницу в геометрии элементов между А и Б падает, т.к. вариативность точек в сумме нивелируется. Ранжирование (два нижних ряда) в принципе позволяет избежать арифметического нивелирования данных и учесть индивидуальные характеристики элементов.

Таким образом, центральной задачей на данном этапе стало определение взаимоувязки геометрических и численных величин, описывающих конкретный элемент. Цель - составление выборок численных (т.е. вычисляемых либо измеряемых) данных, отображающих в трехмерной (в простейшем варианте – двухмерной) системе координат геометрию изучаемого элемента крупно и детально. Это означает, что в массив данных X’,Y’,Z’ или X’,Y’ по выборке из N элементов вносятся как характеристики формы в целом – напр. лемеха «городком», так и флуктуации точек, описывающих точные границы Xi, Yi, Zi как индивидуальный «портрет» каждого элемента выборки А и Б ( рис. 1). [текст с сайта музея-заповедника "Кижи": http://kizhi.karelia.ru]

3. Пробные образцы для анализа и методика их сравнения

При первом взгляде на рис.1 становится видно, что по существу величины X’, Y’, Z’ для каждой выборки могут быть вычислены как арифметическое среднее Xi, Yi, Zi, и тем самым задача частично упрощается до традиционной статистики с вычислением средних X’, Y’, Z’ и характеристик распределения Xi, Yi, Zi – дисперсии и т.д. Таким образом, наиболее критичным является составление выборок по группам образцов 1, 2, 3 и т.д., с тем, чтобы вычисление средних X’, Y’, Z’ в каждой группе было корректным (равноценным) по отношению к другой группе. На практике это достаточно сложно обеспечить. Либо для анализа нужны детали непосредственно, т.е. отдельные лемеха и т.д., либо анализ можно проводить по фото (только для X’, Y’) при условии равнозначности изображений. Ракурс съемки, количество элементов должны максимально совпадать, и также необходим эталон линейного сравнения.

Следовательно, применение методов ранжирования, т.е. непараметрических, для данной задачи неизбежно. Очевидно, что в случае формального учета средних величин координат граничных точек X’, Y’, Z’ за счет различий в габаритах внутри выборки в целом средние величины для разных выборок А и Б будут сближаться по мере увеличения числа образцов и искомый результат найден не будет. Если же составить максимально «корректную» ранговую выборку – так, для лемеха это будет попарное увязывание друг с другом образцов сходных общих габаритов – и затем сравнить ранговые различия выборок А и Б, то есть основания предположить, что выявление статистических различий зафиксирует разное качество выборок А и Б (возможно, видимое глазом).

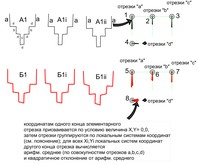
Далее, автором предложено не проводить сравнение i-той пары образцов элементов в ранговой выборке в непосредственном виде суммы разрозненных средних величин X’, Y’, Z’ – т.е. средних координат вершин многоугольника (лемеха). Для сравнения используется модифицированное сочетание средних X’, Y’, Z’ и параметров разброса (дисперсия, квадратичное отклонение и т.д.). Принцип составления модифицированного сочетания данных представлен на рис. 2. Выбрано равное число отрезков границ элемента (для двухмерной системы X, Y), причем сравниваемые отрезки должны по смыслу быть одинаковыми: например, это три нижние зуба городка – их внешние границы по передней поверхности. Далее все «вертикальные» отрезки совмещаются в один пучок с общим началом в условной точке X, Y = 0,0, допустим, в «0,0» локальных координат помещены верхние концы отрезков. Аналогично все «горизонтальные» отрезки – форма границ лемеха – искусственно разделяется на отрезки, совмещенные, предположим, левым концом в точке «0,0». Тогда по «свободным» концам отрезков, учитывая их модифицированные координаты Xii, Yii, можно сравнить средние X’, Y’ и разброс (квадратичное отклонение) относительно каждого X’ и Y’ (рис.2).

Рис. 2. Принцип составления «модифицированных» сочетаний данных о геометрии разного лемеха (условный пример). Составляются ранжированные пары по принципу максимального геометрического и габаритного сходства по выборкам – т.е. пары А1-Б1, А1i – Б1i, А1ii – Б1ii и т.д. Дальнейшие вычисления производятся только для собранных парами рядов. Одинаковые по местоположению отрезки границ формы копируются от образца в локальную систему координат, свою для каждой смысловой группы отрезков, т.е. для длинного ребра лемеха, вертикальных ступенек, горизонтальных отрезков и пр. Один конец отрезка, таким образом, получает координаты 0,0 (допустим верхние концы для вертикальных и левые для горизонтальных). Другие концы отрезка образуют (в локальных системах координат) поля Xi, Yi, для которых производится стандартная мат. обработка – среднее и квадр. отклонение. Ранжирование образцов является в данной методике смысловым критерием, позволяющим не смешивать разнородные или существенно отличные по габаритам детали. [текст с сайта музея-заповедника "Кижи": http://kizhi.karelia.ru]

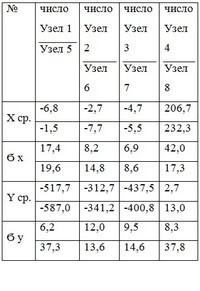
Сравним расчетные величины для локальных систем координат узлов 1–8 рисунка 2 (табл. 1).

Полученные цифры безусловно не идеальны, но они демонстративны хотя бы для простейших случаев – условно «станочного» (выборка А) и «рубленого вручную» (выборка Б) лемеха, т.е. методика в принципе оправдывает ожидание как потенциальный инструмент для диагностики геометрической специфики тех или иных деревянных элементов. Выборка «А» и выборка «Б» получают численные статистические различия в дополнение к визуально-эмпирическим. Критически важным для получения адекватных результатов является корректное ранжирование элементов в сравниваемых выборках (в том числе и деление выборок на части в соответствие с группами элементов по габаритам и геометрии).

4. Вывод:

Рассмотренные простейшие примеры позволяют предполагать, что поиск сочетаний приемов непараметрической и традиционной параметрической статистики для анализа аутентичности геометрии деревянных деталей, как памятников, так и новодела, имеет методический смысл. На первое место выходит поиск адекватных приемов ранжирования образцов, т.е. приемов непараметрической статистики, с возможным последующим обсчетом данных традиционными параметрическими методами. В перспективе разработка алгоритма анализа геометрии деревянных деталей позволит создать как инструменты диагностики аутентичности на базе ЭВМ, так и библиотеки данных, сопровождающих музейные объекты, т.е. библиотеки виртуального цифрового фиксирования памятников. Это позволит решать вопросы реконструкции утраченных фрагментов объектов.

• [1]  Ополовников А.В. Сокровища Русского Севера. М., 1989. С. 9–35.
• [2]  Петров-Спиридонов Н.А. Возможная методика диагностики достоверности воспроизведения подлинной геометрии деревянных деталей в ходе реставрации Преображенской церкви в Кижах // Наука, образование и экспериментальное проектирование. Тез. докл. междунар. науч.-практ. конф. профессорско-преподавательского состава, молодых ученых и студентов 4–8 апреля 2016 г. М., 2016. С. 251.